AdaContrast: Contrasitive Test-Time Adaptation (CVPR 2022)

본 포스팅은 Contrasitive Test-Time Adaptation논문의 리뷰를 다루고 있습니다.

해당 논문의 concept위주로 핵심만 다루고자 합니다.

 

 

Summary

• Test-time adaptation  = source-free adaptation
• self-supervised contrastive learning을 통해 target feature learning을 수행 (w/ pseudo-labeling)
• 동시에, 1) online pseudo-labeling과 2) pseudo labeling refinement를 수행하며 pseudo-labeling을 denoising함 (중점적으로 봐야할 사안―어떻게 pseudo label을 refine하는지?)
• closed-set source-free unsupervised domain adaptation

 

 

Method

: source model은 cross-entropy w/ label smoothing으로 학습된 모델 → target model은 source model의 parameter로 initialized됨

 

 

Framework overview

 

 

component별로 따로따로 살펴보자 (divide & conquer)

 

 

 

 

(a) Online pseudo label refinement

• target image ($x_t$)를 weekly augmentation($t_w$)한 후 encoding된 feature vector(=$w$)를 memory queue에 저장
• 이 $w$의 pseudo-label은 이 것과 가까운 sample들(=nearest neighbor)을 뽑아 softmax probability를 도출하여 average한 값으로 사용함
• 이를 매 mini-batch마다 반복함 (online)

 

• Memory queue
  • length, $M$
  • initialization은 randomly selected M target samples로 수행함
  • queue에는 1) weakly augmented feature와 2) predicted probability를 저장 $\{w'^j, p'^j\}^M_{j=1}$
  • update는 MoCo방식과 동일하게 수행―$(1-m)$만큼만 이전 parameter를 고려하도록 함
• Nearest-neighbor soft voting
  • current classifier의 decision이 불확실할 때, knowledge aggregation을 통해 more informed estimation을 수행하자는 취지
  • Memory queue가 target feature space를 잘 representation하도록 (즉, 좋은 representation feature들이 저장되도록) 발전되고 있다는 가정
  • $w$의 Nearest neighbor는 바로 이 memory queue에서 cosine distance를 기반으로 찾게 됨
  • 그리고 이 neighbor들의 (predicted) probability들을 average하여 만들어진 probability를 통해 pseudo label을 만듦 (pseudo label자체는 argmax이므로 hard)

 

 

 

 

 

(b) Joint self-supervised contrastive learning

• Pretext task : instance discrimination
  • 같은 이미지에 대한 다른 뷰 (augmented image)들은 feature간 가깝게 유지하는 반면, 다른 이미지에 대한 뷰(다른 뷰일수도, 같은 뷰일수도―random 선택이기 때문에)들 feature는 멀게 학습함
  • 위 그림에서 target image에 대한 서로 다른 (strong) augmentation 이미지를 만들어서 MoCo를 수행함 (참고: https://sumniya.tistory.com/39)
• Encoder는 source encoder로 initialization함
  • 이렇게 되면 source로부터 학습된 weight에 있는 knowledge들이 target에서 수행하고자하는 contrastive learning의 좋은 출발점을 마련해 줌 (an informative feature space)
  • 그럼으로써, 약간의 epoch만으로도 converge함 (training cost가 적용)
• 위 그림에서 momentum encoder는 memory queue를 update할 때 사용하는 것과 동일함
  • 위 그림에서 $[k_1, k_2, k_3, ..., k_M]$은 memory queue임 (memory queue가 두 개―여기서는 $Q_{s'}$ (a)에서는 $Q_W$)
  • 단, 구분지어야하는 것은 (a)에서는 weakly augmented encoded feature들을 저장한 것과는 다르게 strongly augmented image를 저장함 ($k_{1 \sim M}$: strongly augmented image features)
  • 여기에 strong augmented view, $k'$를 concat한 후 다음 과정을 수행
• Exclusion of same-class negative pairs
  • 하나의 target image로부터 각기 다른 strong aug.를 진행한 이미지를 각각 encoding한 값 q, k에 대해서, MoCo에서는, cosine distance기반 contrastive learning을 하였음
  • MoCo에서 발전시켜, 현재 이미지($x_t$)와 같은 class인 sample들을 queue에서 제거함―이때, (a)에서 사용된 soft voted pseudo label을 사용함
  • 같은 class인 sample들을 골라내기 위해서, memory queue에 있는 feature(=$k$)들의 pseudo label도 저장함
    • (a)에서 다루었던 memory queue가 weakly augmented feature($w$)와 그에 대한 predicted probability를 저장했다면,
    • 여기서 사용하는 memory queue에는 stronly augmented feature($k$), pseudo label(predicted label)이 저장됨
  • negative sample을 제외하기 위하여 다음과 같이 negatvie sample set을 구성함
    $$\mathcal{N}_q = \{j|1 \leq j \leq P, j \in Z, \hat{y} \neq \hat{y}^j \} \cup \{0\}$$
    • 위 memory queue와 다르게 length를 P로 둠 (그림에는 M으로 되어있음)
    • $\mathcal{N}_q$는 결국 index set
    • 기존에 memory queue에 있던 P개의 strongly augmented feature $k_{1 \sim P} $에 새로운 $k$가 concat됨 → 이는 query와 동일 image에서 augmented image feature이므로 index set에 추가됨 (그래서 $\cup \ \{0\} $ 을 해줌―결국 이게 $k_+$)
• Contrastive learning loss, $L^{ctr}_t$

$$ L^{ctr}_t = L_{InfoNCE} = - \log \frac{\exp q\cdot k_+ / \tau}{\sum_{j \in N_q} q \cdot k_j / \tau} $$

 

 

 

 

 

(c) Additional regularization

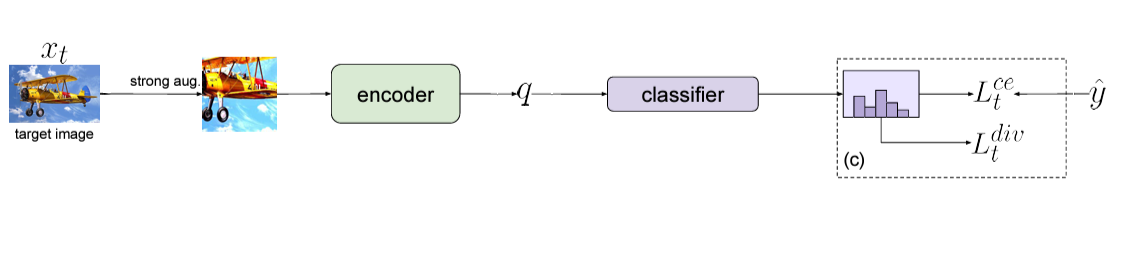
• Weakly-strong consistency, $L^{ce}_t$ : FixMatch―weak/strong augmented image의 prediction probability entropy를 줄이는 self-supervised learning방법―처럼 같은 이미지에서 나온 $\hat{y}$(pseudo label from $w$)과 $q$의 CE loss를 걸어 이 차이를 줄임
  $$ L^{ce}_t  = - \mathbb{E}_{x_t \in \chi_t} \sum^C_{c=1} \hat{y}^c \log p^c_q$$
  where $p_q$=$\sigma(g_t(t_s(x_t)))$ are the predicted probabilities for the strongly-augmented query image $t_s(x_t)$ 

 

• Diversity regularization, $L^{div}_t$ : 혹시 과정 상에 발생하는 false label을 모델이 학습하는 것을 방지하기 위해 class diversification term을 추가함
  $$ L^{div}_t  = \mathbb{E}_{x_t \in \chi_t} \sum^C_{c=1} \bar{p}^c_q \log \bar{p}^c_q $$
  $$ \bar{p}^c_q = \mathbb{E}_{x_t \in \chi_t} \sigma(g_t(t_s(x_t))) $$